1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
%question1.m
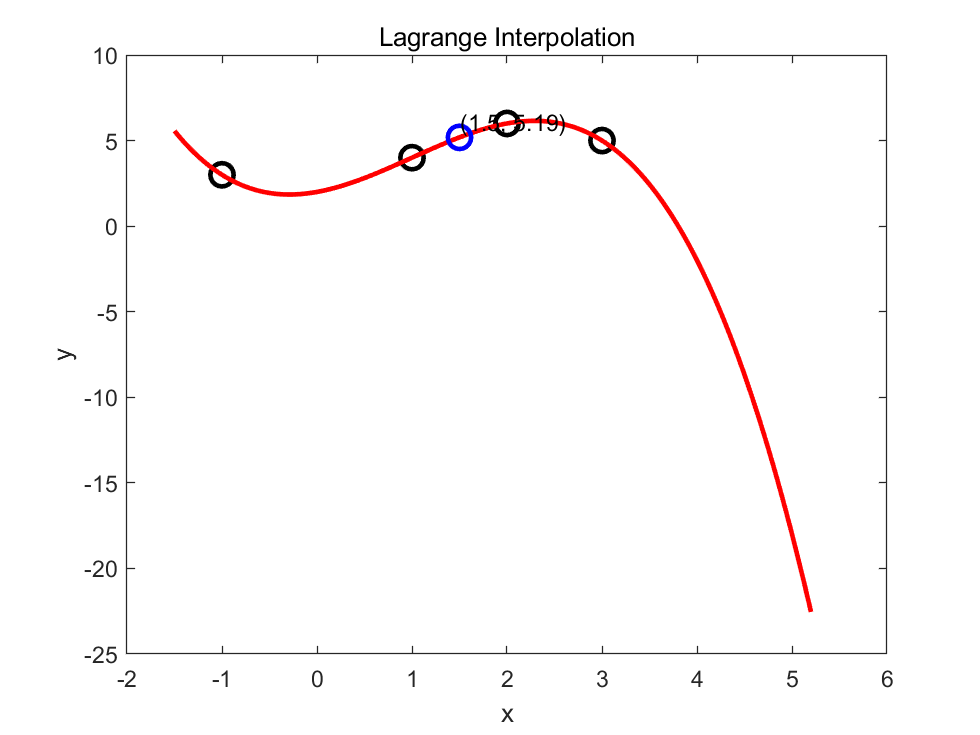
x=-1.5:0.01:5.2; % 加密数据点
xdata=[-1,1,2,3]; % 已知数据点
ydata=[3,4,6,5]; % 点 xdata 处的函数值
y=lagrange_interp(xdata,ydata,x); % Lagrange 插值
% 计算在 x = 1.5 处的预测值
x_pred = 1.5;
y_pred = lagrange_interp(xdata,ydata,x_pred);
% 绘制图形
figure; % 创建新的图形窗口
plot(xdata,ydata,'ko','MarkerSize',10,'LineWidth',2); % 绘制原始数据点,设置点的大小和线宽
hold on; % 保持当前图形,以便在同一图形上添加更多的线或点
plot(x,y,'r','LineWidth',2); % 绘制拉格朗日插值的结果,设置线的颜色和线宽
plot(x_pred,y_pred,'bo','MarkerSize',10,'LineWidth',2); % 绘制预测点,设置点的颜色、大小和线宽
text(x_pred,y_pred,sprintf('(%0.1f, %0.2f)',x_pred,y_pred),'VerticalAlignment','bottom'); % 在图上显示预测值
hold off; % 取消保持图形
% 添加标题和轴标签
title('Lagrange Interpolation');
xlabel('x');
ylabel('y');
|