北邮Matlab选修期中作业

题目 #1

问题描述

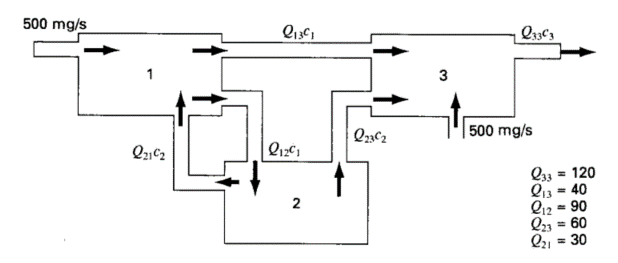
下图给出了一个用管道连接的三个反应的系统。如图所示，化学物质通过每个管道传输的速率等于流率Q(单位为$m^3/s$)乘以导致流动的反应浓度c(单位为$mg/m^3$)。如果系统状态稳定，则每个反应输入的化学物质和输出的达到平衡。为每个反应构建质量平衡方程，并求解得到它们的浓度。

数学模型

数学关系

对于所有的反应，在稳定状态时，都有流入的速率等于流出的速率，以此为基础，可以得到三个方程如下：

反应 #1

$$ 500+Q_{21}c_2 = Q_{12}c_1 + Q_{13}c_1 $$
反应 #2

$$ Q_{12}c_1=Q_{21}c_2+Q_{23}c_2 $$
反应 #3

$$ 500 + Q_{13}c_1+Q{23}c_2=Q_{33}c_3 $$

化简并得到对应方程

其中：

$ Q_{33}=120$,$Q_{13}=40$,$Q_{23}=60$,$Q_{21}=30$

替换并转化成矩阵形式如下：

程序设计

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


%Guass.m
function [U,x]=Gauss(A,b)
% 顺序Gauss消去法求解线性方程组
% 输入参数：
%---A：线性方程组的系数矩阵
%---b：线性方程组的右端项
% 输出参数：
%
%---U：消元后的上三角方程组的增广矩阵---x：线性方程组的解
n=length(b);
% 消元过程
for k=1:n-1 % 消元成上三角矩阵
  m=A(k+1:n,k)/A(k,k);
  A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-m*A(k,k+1:n);
  b(k+1:n)=b(k+1:n)-m*b(k);
  A(k+1:n,k)=zeros(n-k,1);
end
U=[A,b];
% 回代过程
x=zeros(n,1);
x(n)=b(n)/A(n,n); % 求x_n
for k=n-1:-1:1 % 回代
  x(k)=(b(k)-A(k,k+1:n)*x(k+1:n))/A(k,k); % 求 x_k，k=n-1,n-2,…,1
end

计算结果

1
2
3
4
5


%test1.m
A=[130,-30,0;90,-90,0;40,60,-120];
b=[500;0;-500];
[U,c]=Gauss(A,b);
disp(c);

题目 #2

问题描述

下面给出了一个迭代模型：

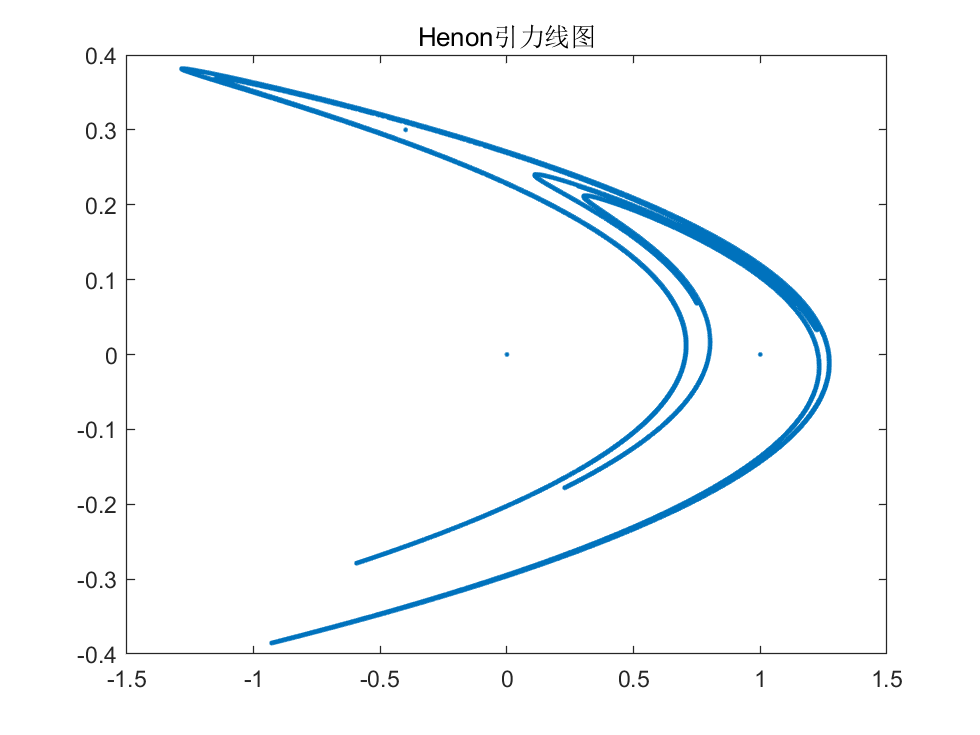
写出求解该模型的M函数。如果迭代初值为$x_0=y_0=0$，那么，进行30000次迭代求出一组$x$和$y$向量，然后在所有的$x_k$和$y_k$坐标处画一个点（注意不要连线），最后绘制出所需的图形（说明：这样绘制出的图形称为Henon引力线图，它将迭代出来的随机点吸引到一起，最后得出貌似连贯的引力线图）。

程序设计

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


%Henon.m
function XY=Henon(x0,y0,N)
% Henon引力线
% 输入参数：
%
%---x0：迭代初始值-x0
%---y0：迭代初始值-y0
%---N：迭代次数
% 输出参数：
%
%---XY：Henon引力线的点坐标
x=x0;
y=y0;
% 初始化存储结果的矩阵，第一行存储初始值
XY = [x0, y0];

% 迭代模型
for k = 1:N
    % 更新x和y的值
    x_new = 1 + y - 1.4 * x^2;
    y_new = 0.3 * x;
    
    % 将新的x和y值添加到矩阵的下一行
    XY = [XY; x_new, y_new];
    x=x_new;
    y=y_new;
end

% 绘制Henon引力线图
figure;
plot(XY(:,1), XY(:,2), '.'); % 绘制点，不连线
title('Henon引力线图');

计算结果

1
2
3
4


%test2.m
x0=0;y0=0;%定义初始值
N=30000;%迭代次数
XY=Henon(x0,y0,N);%调用函数

1

>> test2

Matlab 期中作业

BUPT大一下Matlab选修

北邮Matlab选修期中作业

题目 #1

问题描述

数学模型

数学关系

化简并得到对应方程

程序设计

计算结果

题目 #2

问题描述

程序设计

计算结果

北邮Matlab选修 期中作业

题目 #1

问题描述

数学模型

数学关系

化简并得到对应方程

程序设计

计算结果

题目 #2

问题描述

程序设计

计算结果

北邮Matlab选修期中作业